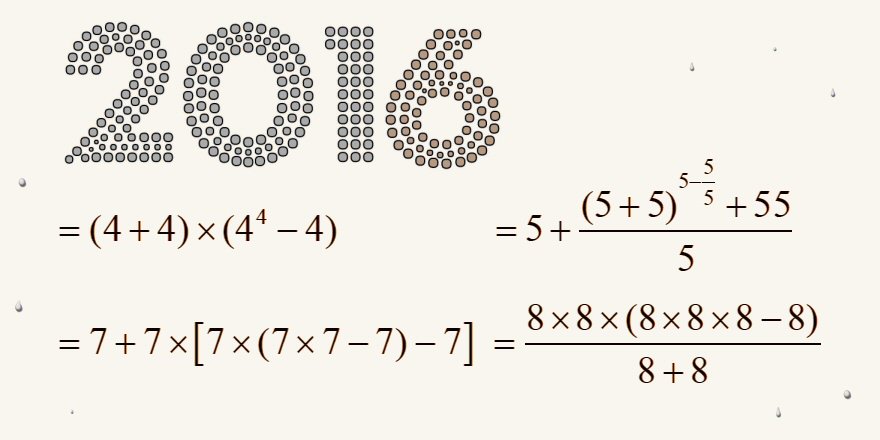Cette année, les mathématiciens ont de quoi s'amuser. Le nombre 2016 possède 783 propriétés intéressantes.
Pour
prédire une année spéciale, certains se fient aux boules de cristal.
D'autres, aux mathématiques. Et pour 2016, ceux-là auront plus d'un
argument à leur disposition. Ils en auront même au moins 783, puisque
c'est le nombre de propriétés intéressantes que comporte le nombre 2016.Comme l'explique le blogueur El Jj, 2016 est un nombre dit triangulaire: on peut représenter un triangle composé de 2016 points puisque 1+2+3+4+...+63 = 2016. Mieux: 2016 n'est pas seulement triangulaire, il est hexagonal. Ce qui correspond à la formule 2 x 32² – 32 = 2016.
Le site FindTheFactors souligne qu'en plus d'être égal à la somme de tous les chiffres de 1 à 63, 2016 équivaut à la somme de plusieurs suites, notamment 671 + 672 + 673 = 2016 ;
285 + 286 + 287 + 288 + 289 + 290 + 291 = 2016 ;
ou encore 86 + 87 + 88 + 89 + 90 + 91 + 92 + 93 + 94 + 95 + 96 + 97 + 98 + 99 + 100 + 101 + 102 + 103 + 104 + 105 + 106 = 2016.
==============================
728 Number Facts and Factors of the Year 2016
2016 is the sum of all the counting numbers from 1 to 63. That makes 2016 the 63rd triangular number which can be calculated rather quickly using 63 x 64/2 = 2016. That is definitely an example of multiplication being a shortcut for addition!
Besides being the sum of the counting numbers from 1 to 63, 2016 is the sum of consecutive numbers a few other ways as well:
- 671 + 672 + 673 = 2016; that’s 3 consecutive numbers.
- 285 + 286 + 287 + 288 + 289 + 290 + 291 = 2016; that’s 7 consecutive numbers.
- 220 + 221 + 222 + 223 + 224 + 225 + 226 + 227 + 228 = 2016; that’s 9 consecutive numbers.
- 86 + 87 + 88 + 89 + 90 + 91 + 92 + 93 + 94 + 95 + 96 + 97 + 98 + 99 + 100 + 101 + 102 + 103 + 104 + 105 + 106 = 2016; that’s 21 consecutive numbers.
2016 is also the 32nd hexagonal number
because 2 x 32² – 32 = 2016. (All hexagonal numbers are also triangular
numbers, and half of all hexagonal numbers are triangular numbers.)
2016 is not a palindrome in any bases until base 47. We just need a
symbol to represent 42 base 10 in base 47 because 42(47) + 42(1) = 2016.The last two years on New Year’s Eve I have predicted the factors of the coming year. Each time my predictions were 100% accurate. I am now ready to make my predictions for the factors of 2016: (Drum roll) There will be 36 positive factors for 2016:
1, 2, 3, 4, 6, 7, 8, 9, 12, 14, 16, 18, 21, 24, 28, 32, 36, 56, 63, 72, 84, 96, 112, 126, 144, 168, 224, 252, 288, 336, 504, 672, 1008, 2016. Sadly, if you multiply any of them by -1, you’ll know a negative factor for 2016, too.
The factors of 2016 will also come in pairs: 1 x 2016, 2 x 1008, 3 x 672, 4 x 504, 6 x 336, 7 x 288, 8 x 252, 9 x 224, 12 x 168, 14 x 144, 16 x 126, 18 x 112, 21 x 96, 24 x 84, 28 x 72, 32 x 63, and 36 x 56.
Because the number of 2016’s prime factors is a power of two, 2016 can make a nicely proportioned factor tree especially if we use any of the factor pairs that are in red. (14 x 114 is in bold only because I like the way it looks.) Because 2016 has 8 prime factors, we can get a very full and impressive tree. For example:

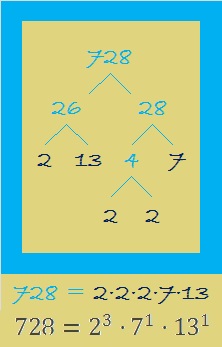
Since this is my 728th post, I’ll write a little about the number 728, too. I’ll start with this factor tree for 728:
It’s not as impressive as the factor tree
for 2016, but did you notice that 2016 and 728 share several of the same
prime factors?
When two numbers share some of the same
factors, we may wonder what is the greatest common factor and what is
the least common multiple?
One way to find either value is to use the
prime factorization of both numbers. The prime factorization of 2016
uses three bases: 2, 3, and 7, while the prime factorization for 728
uses these bases: 2, 7, and 13. Write down all those bases without
duplication, and you get 2, 3, 7, and 13.
For the GREATEST COMMON FACTOR (GCF), look
at the prime factorizations and choose the SMALLEST exponent that
appears in each. The greatest common factor cannot be bigger than the
smallest number, 728. In this case it is 56 which will divide evenly
into both 728 and 2016.
For the LEAST COMMON MULTIPLE (LCM), look at the prime factorizations
and choose the LARGEST exponent that appears in each. The least common
multiple cannot be smaller than the largest number, 2016. In this case
it is 26,208 which both 728 and 2016 can divided into evenly.This method for finding the GCF and LCM will also work for three, four, or more numbers and even variable bases like x, y, or z. I encourage you to give it a try!
Here are some more number facts about the number 728:
26 x 28 = 728, and both 26 and 28 are one number away from 27, their average, so 728 is one number away from 27².
Here’s proof: 26 x 28 = (27 – 1)(27 + 1) = (27² – 1²) = 729 – 1 = 728.
Because 13 is one of its prime factors, 728
is the hypotenuse of Pythagorean triple 280-672-728. The greatest common
factor of those three numbers is the same as the greatest common factor
of 728 and 2016, but what is their least common multiple? It turns out
to be 5 x 12 x 13 x 56, the product of the numbers in the primitive
Pythagorean triple, 5-12-13, and 56. Using prime factorizations we get
(2^5)(3^1)(5^1)(7^1)(13^1). We get the same answer using either method.
728 is a palindrome (repdigit) in three other number bases:
- 728 is 222222 BASE 3; note that 2(3^5) + 2(3^4) + 2(3^3) + 2(3^2) + 2(3^1) + 2(3^0) = 728.
- 888 BASE 9; note that 8(81) + 8(9) + 8(1) = 728.
- QQ BASE 27 (Q = 26 base 10); note that 26(27) + 26(1) = 728.
————————————————
- 728 is a composite number.
- Prime factorization: 728 = 2 x 2 x 2 x 7 x 13, which can be written 728 = (2^3) x 7 x 13
- The exponents in the prime factorization are 1, 3, and 1. Adding one to each and multiplying we get (1 + 1)(3 + 1)(1 + 1) = 2 x 4 x 2 = 16. Therefore 728 has exactly 16 factors.
- Factors of 728: 1, 2, 4, 7, 8, 13, 14, 26, 28, 52, 56, 91, 104, 182, 364, 728
- Factor pairs: 728 = 1 x 728, 2 x 364, 4 x 182, 7 x 104, 8 x 91, 13 x 56, 14 x 52, or 26 x 28
- Taking the factor pair with the largest square number factor, we get √728 = (√4)(√182) = 2√182 ≈ 26.981475.
Par ailleurs, le site Number Empire fait ressortir que 2016 est divisible par 1,2,3,4,6,7,8 et 9. En fait, il est divisible par 32 nombres entiers. C'est cette particularité qui lui confère autant de propriétés intéressantes. En comparaison, les nombres 2013, 2014 et 2015 en possèdent entre 4 et 7 fois moins.
Sur Twitter, les matheux ont donc pu présenter leurs voeux... à leur façon.
For lovers of mathematics, Happy 2016! (from @IJTANEJA)