Grigori Perelman: le génial mathématicien russe a résolu l'un des 7 problèmes du millénaire

Grigori « Grisha » Perelman avait travaillé sur le sujet dans son Saint-Pétersbourg natal, où il était revenu en 1995 après avoir vécu quelques années aux États-Unis.
Il y a plus d'une décennie , Grigori Perelman, l'un des grands cerveaux du XXIe siècle, a dit « au revoir » à sa profession et à la vie publique. Il avait refusé la prestigieuse médaille Fields et un prix d'un million de dollars.
À ce moment-là, il était déjà mondialement connu pour avoir résolu l'une des énigmes mathématiques les plus difficiles dont les origines remontent au 18ème siècle.

L'ancienne ville prussienne de Königsberg -aujourd'hui Kaliningrad, en Russie- avait sept ponts, car la rivière Pregel non seulement la traversait, mais aussi bifurquait, créant une île et la divisant en quatre régions.

Dans la ville de Königsberg, les intellectuels avaient un curieux passe-temps dominical.

Comme un jeu pour les intellectuels de l'époque, une question fut formulée qui deviendra un célèbre problème mathématique :

Est-il possible de partir à pied depuis n'importe laquelle des quatre régions de Königsberg, en traversant tous les ponts une fois et en revenant au même point de départ ?

Trouver la solution s'est avéré beaucoup plus difficile qu'il n'y paraît.

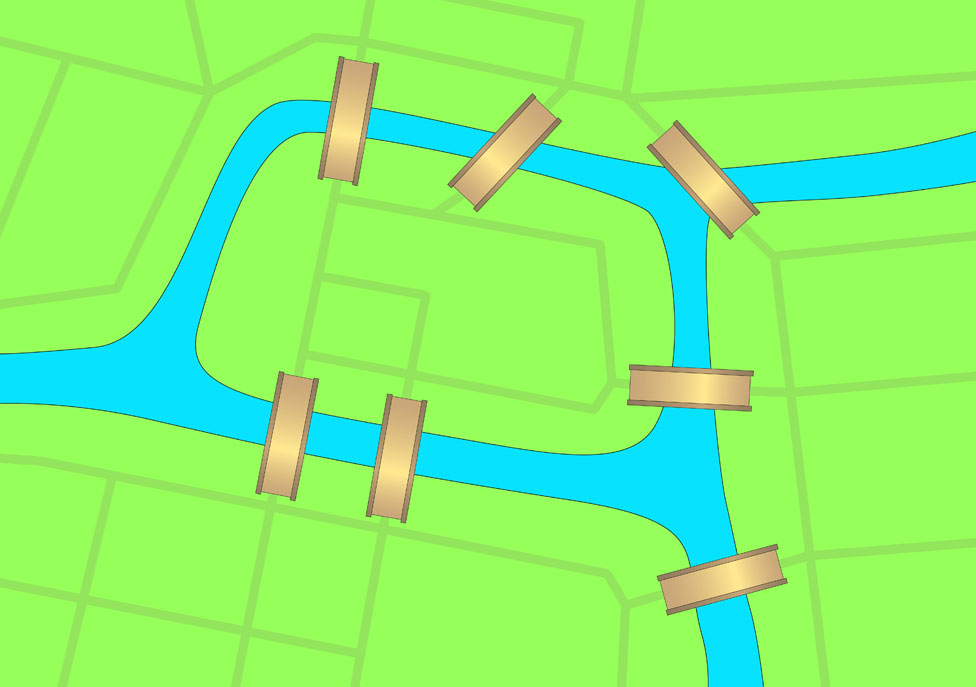Le pont du forgeron, le pont de liaison, le pont vert, le pont du marché, le pont en bois, le pont haut et le pont du miel ne pouvaient être traversés qu'une seule fois sur la promenade.

Finalement, en 1735, le grand mathématicien Leonhard Euler a donné la réponse : ce n'était pas possible.

Pour résoudre le problème, il a fait un saut conceptuel.

Il s'est rendu compte que les distances entre les ponts n'étaient pas pertinentes; ce qui importait vraiment , c'était la façon dont les ponts étaient reliés les uns aux autres .

La solution d'Euler était importante car elle s'appliquait non seulement à la ville de Königsberg, mais aussi à toutes les configurations topologiquement identiques.

Topologiquement ?

Cette solution au puzzle a ouvert les portes à un nouveau type de géométrie positionnelle : la topologie .

Cela peut sembler très étranger, mais beaucoup d' entre nous bénéficient de la topologie au quotidien .

Pratiquement toutes les conceptions de plans de métro dans le monde sont basées sur des principes topologiques, afin de communiquer clairement ce que les utilisateurs doivent savoir : comment se rendre là où ils veulent aller.

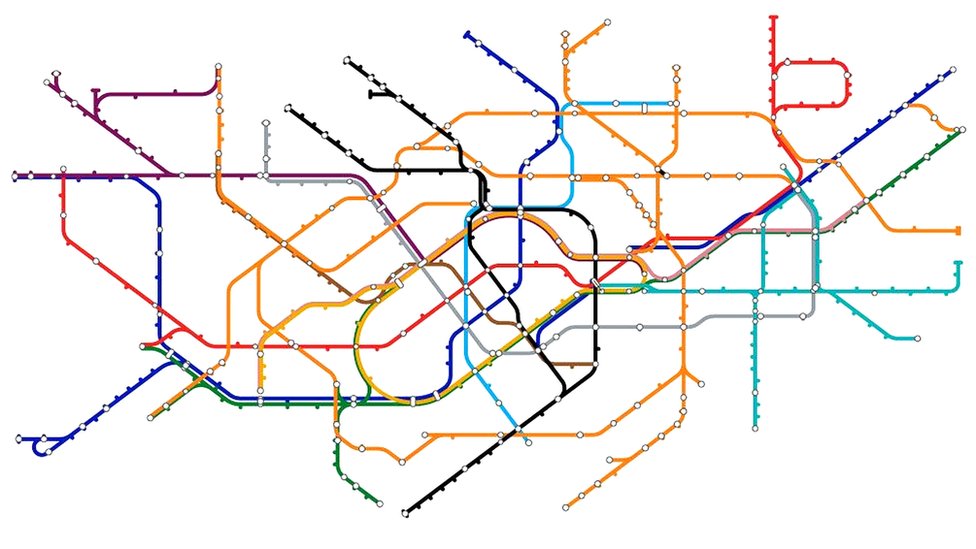Ce que vous devez savoir, c'est comment vous rendre d'où vous êtes à l'endroit où vous voulez aller, donc - bien que cela vous donne une idée des distances - ce qui compte, c'est que vous voyiez clairement les connexions.

Bien que la topologie ait ses origines dans les ponts de Königsberg, c'est entre les mains du plus célèbre et respecté des mathématiciens de la fin du XIXe siècle, le Français Henri Poincaré , que le sujet s'est développé en une nouvelle façon puissante de regarder la forme .

À peu près

L'idée principale derrière la topologie est que lors de l'étude d'un objet, ce sont ses propriétés qui sont importantes , pas l'objet lui-même , et si deux objets partagent les mêmes propriétés, ils doivent être étudiés, car les résultats s'adapteront à tous les objets qu'ils partagent. ces propriétés, appelées objets homéomorphes.

Certaines personnes appellent cet important domaine des mathématiques la « géométrie flexible » car, selon lui, deux formes sont identiques si vous pouvez transformer l'une en l'autre sans la casser.

Ainsi, par exemple, topologiquement un ballon de football et un ballon de rugby sont équivalents car l'un peut se transformer en l'autre.

Si le rugby est arrondi...

C'est pourquoi on dit d'un topologue qu'il est une personne qui ne sait pas faire la différence entre sa tasse de café et son beignet .

Et c'est que, bien que cela semble étrange, topologiquement une tasse et un beignet sont les mêmes.

Sans casser le beignet, vous pouvez le transformer en gobelet,
mais pas en boule, car le trou ne le permet pas.

Mais, s'il est possible de déformer un beignet en gobelet et vice versa, il n'y a aucun moyen de déformer une boule en beignet car nous ne pouvons pas créer le trou dans le beignet sans changer les propriétés de la sphère.

Le problème

Poincaré en vint à connaître toutes les surfaces topologiques bidimensionnelles possibles.

De plus, il a développé toutes les manières possibles d'envelopper cet univers plat en deux dimensions.

Mais nous vivons dans un univers tridimensionnel, alors en 1904, se demandait-il, quelles sont toutes les formes possibles que notre Univers peut avoir ?

Il tenta de trouver la réponse mais mourut en 1912 sans succès.

Le français Henri Poincaré (1854-1912), est considéré comme l'un des meilleurs mathématiciens de tous les temps. Il a travaillé sur la mécanique céleste, la topologie, la relativité et est considéré comme le fondateur de la théorie du chaos. Il a également soulevé la conjecture de Poincaré, en 1904, un problème de topologie difficile à résoudre.

Ce problème topologique a conduit à ce qui est devenu connu sous le nom de conjecture (ou hypothèse) de Poincaré , et il est resté un héritage pour les générations futures de mathématiciens.

Avec le passage du 20e siècle, des légions de mathématiciens ont tenté de résoudre les problèmes non résolus.

70 ans après la mort de Poincaré, la conjecture avait été résolue pour toutes les autres dimensions sauf la 3D.

Malgré de nombreuses tentatives, le siècle s'achève mais l'inconnue persiste, et la conjecture de Poincaré est incluse dans la liste des sept problèmes mathématiques du millénaire dont la résolution sera récompensée d'un million de dollars par le Clay Institute of Mathematics du Massachusetts, USA.

Deux ans plus tard, le 11/11/2002, le premier des trois volets d'un article intitulé "La formule d'entropie pour le flux de Ricci et ses applications géométriques" est apparu sur le site Web public arXiv.

Dans son intégralité, le texte s'étendait sur 39 pages et était signé par Grisha Perelman .

Peu orthodoxe

Grigori « Grisha » Perelman avait travaillé sur le sujet dans son Saint-Pétersbourg natal, où il était revenu en 1995 après avoir vécu quelques années aux États-Unis car, racontait-il à un collègue, il s'était rendu compte qu'il travaillait mieux en Russie .

"Grisha" est né en 1955,
lorsque Saint-Pétersbourg
s'appelait Leningrad
et se trouvait en
Union soviétique.

Il n'était pas inconnu de la communauté mathématique : en 1994, il avait prouvé la conjecture d'Alma , qui énonce que l'on peut déduire les propriétés d'un objet mathématique à partir de petites régions de ces objets, appelées âmes.

Après cela, il s'est vu offrir des postes dans certaines des plus grandes universités du monde, dont Stanford et Princeton, mais a préféré occuper un poste de chercheur à l'Institut Steklov de Saint-Pétersbourg, qui payait moins de cent dollars par mois.

De son voyage aux États-Unis, il avait retiré, disait-il, assez d'argent pour bien vivre.

Mais il a aussi emporté une question soulevée par un mathématicien américain qu'il admirait : Richard Hamilton.

Des flux qui n'ont pas coulé

En 1982, Hamilton avait publié un article sur une équation appelée le flux de Ricci, dont il soupçonnait qu'elle pourrait prouver la conjecture de Poincaré.

Mais la tâche était extrêmement technique et son exécution compliquée.

En 1993, Perelman a accepté une bourse Miller à l' Université de Californie à Berkeley , et pendant son séjour, il a assisté à plusieurs des conférences de Hamilton.

À la fin de l'un d'entre eux, Hamilton a parlé à Perelman du plus gros obstacle qu'il avait rencontré en essayant de prouver la conjecture, et le Russe a souligné qu'il avait fait une étude qui pourrait l'aider à le surmonter.

Mais Hamilton n'a prêté aucune attention à lui .

Hamilton est connu pour avoir découvert le flux de Ricci et lancé un programme de recherche qui s'est avéré être le sol fertile dans lequel le test Perelman prospérerait, et son génie.

Deux ans plus tard, Perelman a lu un article de Hamilton discutant de certaines de ses idées pour prouver la conjecture de Poincaré et a noté que le mathématicien n'avait fait aucun progrès : il était coincé .

Voulant collaborer, Perelman lui a écrit une longue lettre expliquant ses idées, mais Hamilton n'a jamais répondu.

Perelman a dû travailler seul et ce qu'il a publié sur Internet en 2002 est le résultat de ses efforts.

Il l'a fait!

La publication de Perelman a suscité un énorme intérêt parmi les mathématiciens.

Bien qu'il n'y ait eu aucune mention directe de Poincaré dans son titre ou ailleurs, quatre ans plus tard, un consensus s'est dégagé dans la communauté mathématique : Perelman avait prouvé la conjecture .

Pour présenter en détail la réalisation de Perelman, il a fallu aux mathématiciens John Morgan et Gang Tian un livre entier, qui apparaît ici sur "Assembled Topology" de l'artiste Douglas Ho à Quarry Bay Park.

Si quatre ans semblent une éternité, gardez à l'esprit que nous parlons de mathématiques.

Contrairement à d'autres domaines de la connaissance, où les théories peuvent toujours être révisées, la preuve d'un théorème est définitive , il n'est donc pas surprenant que les au moins deux équipes d'experts qui l'ont examiné aient pris le temps de vérifier qu'il n'y avait pas de lacunes ou d'erreurs significatives. .

De plus, les articles ne contenaient aucune explication ou digression, et sa preuve était si complexe qu'elle était difficile à comprendre même pour les experts .

Par conséquent, l'analyser a pris du temps et du dévouement : l'explication détaillée faite par l'une de ces équipes d'experts qui a examiné ce que Perelman a présenté en 39 pages a occupé 473 pages.

Le silence du génie

Après plus d'un siècle de tentatives avortées, la conjecture d'un brillant mathématicien avait été prouvée par une autre tout aussi brillante, quoique plus original.

Le théoricien russe a été inondé d'offres (d'honneurs, de prix en espèces et de financement de la recherche, ainsi que de nominations universitaires lucratives dans les universités les plus distinguées de la planète et de tournées de conférences mondiales) qu'il aurait trouvées profondément offensantes. .

« La monétisation de la réussite est l'ultime insulte aux mathématiques », a-t-il déclaré.

Le génie a décidé de s'effacer de la vie publique.

Par conséquent, il a tout refusé, y compris la médaille Fields, l'équivalent mathématique d'un prix Nobel, pour "ses contributions à la géométrie et ses idées révolutionnaires" qui ont conduit à sa preuve exceptionnelle, un prix de la Société mathématique européenne et le million de dollars que le Clay Institute a voulu lui confier pour avoir résolu l'un des problèmes du millénaire.

« Si la démo est correcte, vous n'avez besoin d'aucun autre type de reconnaissance », a-t-il expliqué.

« Je ne suis pas intéressé par l'argent ou la célébrité ; Je ne veux pas être exhibé comme un animal dans un zoo ", a-t-il déclaré.

Alors que beaucoup l'ont qualifié de "fou", notamment pour avoir refusé le million de dollars - il y a même un livre qui allègue qu'il souffre d'une forme d'autisme - il y a ceux qui considèrent noble le fait qu'il soit plus intéressé à démontrer  des théorèmes que de  gagner des prix.

Le malheur - pour le progrès scientifique, du moins - est qu'en plus de s'éloigner de la foule déchaînée, il semble qu'il ait effectivement complètement abandonné les mathématiques.

Ou nous surprendra-t-il un jour avec un autre article brillant quelque part sur Internet ?

Source : Par BBC World Publié le 3 juin 2019

Traduction automatique non révisée