L’harmonie d’Or

On l’appel le nombre d’Or, Phi, la divine proportion, le nombre de l’harmonie universelle ou de la création. Mais pourquoi autant de respect sacré, reconnu par toutes les civilisations, à toutes les époques, autour d’un simple chiffre ; =  (1+√5) ÷ 2  ≈  1,6180339887…

L’utilisation de ce chiffre est très ancienne, elle a même peut être été toujours utilisée consciemment ou inconsciemment, depuis que l’homme observe son environnement.

Léonard de Vinci, l’un des plus grands génies de tous les temps, a été le premier à mettre en évidence les proportions idéales et harmonieuses du corps humain, grâce à ses illustrations reprises dans le livre de Luca Pacioli dénommé « La divine proportion », au 15ème siècle. L’intérêt de ce nombre, d’après Luca Pacioli, ne réside pas tant dans ses propriétés mathématiques que mystiques, elles « concordent avec les attributs qui appartiennent à Dieu… ». Pour les mathématiciens de l’époque, et encore maintenant, ce chiffre est irrationnel.

Pour Léonard de Vinci, c’est une clef d’Or qui ouvre les portes de la philosophie, la perspective, la peinture, la sculpture, l’architecture, la musique, les disciplines mathématiques et les hautes et très secrètes sciences de la vie.

Illustration de Léonard de Vinci (Le nombre d’Or dans le corps humain)

Le nombre d’or est une proportion que l’on retrouve dans tous les enseignements artistiques. Il existe une sorte de convention appliquée par tous les artistes du monde et de toutes les époques, qui permet de structurer une œuvre de telle sorte qu’elle respecte des proportions, et des compositions idéales et harmonieuses. Tous les plus grands chefs d’œuvres de la création, reconnus comme étant d’une grande beauté, sont tous basés sur cette divine et majestueuse proportion.

Ce qui est incroyable, c’est que lorsqu’on ne respecte pas cette proportion idéale, la notion de beauté et d’agréable disparaît.

Force est de constater que le nombre d’Or est lié à la beauté et à l’harmonie, ou peut être l’inverse.

La naissance de vénus de Botticelli, construite avec la proportion d’Or

Au XIIIème siècle, un mathématicien italien du nom de Leonardo Fibonacci [1], fit une expérience sur la croissance d’une population de lapin. Les résultats de cette expérience donnèrent une suite de nombres entiers correspondante aux paires de lapereaux engendrés au fil des mois. Cette suite de nombre sera nommée la suite de Fibonacci, et sa découverte est d’une importance capitale.

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, etc …

L’enchainement harmonieux de la suite de Fibonacci

En effet, ce qui est surprenant est que cette suite est présente partout dans la nature. Elle décrit une trajectoire harmonieuse et constante, à partir d’un centre qui se déploie en spirale à l’infinie, comme un vortex. Pour obtenir les chiffres, rien de plus facile, il suffit d’additionner à chaque fois les 2 chiffres précédents. Quand on regarde la proportion de ses 2 chiffres qui permet de calculer le suivant, on s’aperçoit qu’ils correspondent étrangement à la proportion d’or.

Un puriste mathématicien soulignera, à juste titre, qu’au début de la suite de chiffre, cette proximité au nombre d’or est grossière, et ne correspond pas exactement à 1,6180339887…, mais plus les chiffres s’envolent, plus on se rapproche précisément du nombre d’or. Un pur hasard ?

Alors le hasard fait formidablement bien les choses, au point de flirter insolemment avec le surnaturel, ou le divin. La divine proportion porte bien son nom.

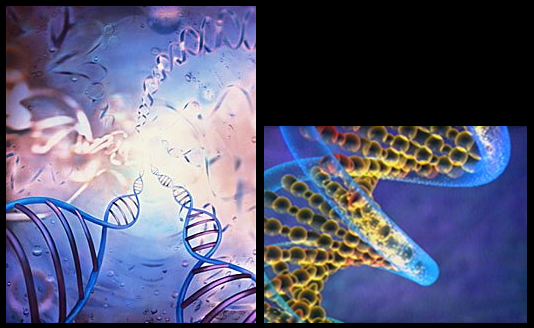Le nombre d’Or dans la molécule d’ADN

Les dimensions de la molécule d’ADN sont également en rapport avec la suite de Fibonacci.

Le rapport entre sa longueur (34 angstroms) et sa largeur (21 angstroms) d’un cycle complet de la double hélice, est égal au nombre d’or.

L’ADN dans la cellule se présente comme une double hélice entrelacée. Cette forme a deux sillons dans ses spirales dans un rapport du nombre d’or entre grand et petit sillons respectivement environ 21 et 13 angstroms. Et on retrouve, comme par hasard, 3 chiffres clés : 13, 21, 34.

Visiblement, la proportion dorée est un modèle pour la nature, dans l’infiniment petit, comme dans l’infiniment grand. Pour s’en convaincre, nul besoin de formules scientifiques complexes, il suffit de contempler la beauté structurelle des quelques images qui suivent.

Cristaux de glace, une décomposition fractale

La suite de Fibonacci dans le cœur des fleurs

Belle représentation de la suite de Fibonacci

Déploiement des branches d’un arbre conformément à la suite de Fibonacci

La spirale de la suite de Fibonacci dans un cyclone

La spirale de la suite de Fibonacci dans une galaxie

La suite de Fibonacci semble fonctionner comme un accélérateur de création, une force qui s’autoalimente continuellement. Généré par une microscopique impulsion cosmique, les forces engendrées on parcourut l’univers depuis l’origine des temps, grandissant et créant des structures fractales (Voir article : La nature, notre déesse à tous) qui véhiculent l’énergie et le temps, à l’échelle de nos galaxies et au-delà, toujours attirées vers un équilibre unique, l’harmonie d’Or.

Source 

[1] Dans "Les Arabes précurseurs de l’ère numérique ?"

Nous avions écrit : 

Transmission des chiffres arabes en Europe et au reste du monde

L’histoire de cette transmission est assez édifiante.

Sachant manipuler les chiffres arabes,
et voulant les introduire chez les chrétiens,
le pape Syslvestre II fut taxé de
diabolique et représenté comme tel !

- Une première tentative a été faite par le pape de l’an 1000, Sylvestre II. Premier pape français, Sylvestre II, né Gerbert d’Aurillac, est aussi un grand savant et un acteur politique majeur. Né vers 945 dans une famille de paysans, Gerbert est éduqué à l'abbaye Saint-Géraud d'Aurillac, dans un esprit moderniste. Remarqué par le comte de Barcelone, le garçon poursuit son instruction dans les abbayes catalanes. Il y découvre le « quadrivium », c'est-à-dire les quatre sciences profanes de son époque : l'arithmétique (dont la numération indo-arabe), la géométrie, la musique et l'astronomie, à travers des manuscrits en latin traduits de l'arabe. Ce faisant, le moine précède de plus d'un siècle les étudiants des universités de Paris, Montpellier et Oxford qui vont au XIIe siècle traverser comme lui les Pyrénées pour compléter leurs connaissances grâce aux maîtres et savants arabes. Devenu pape en 999, sous le nom de Sylvestre II, il use de toute son autorité pour imposer les chiffres arabes chez les chrétiens, à la place des chiffres romains peu pratiques. Sa tentative va échouer, à cause de la résistance des "savants" de l’Église (que l'on peut comparer aux "savants" wahhabites d'Arabie ou ceux de "l'Etat Islamique" de nos jours) , qui considéraient que tout ce qui venait des Sarrasins (les Arabes) ne pouvait qu’être diabolique. On accusa même ce pape d’être habité par le diable. Cette légende a eu la vie tenace, à tel point qu’en 1648, six siècles plus tard, l’autorité pontificale fit ouvrir le tombeau de Sylvestre II pour vérifier si les diables de l’enfer ne l’habitaient point !

- Deux siècles plus tard, une deuxième tentative va réussir.

Né à Pise en Italie, Leonardo Fibonacci (1175-1250), a été élevé et éduqué en grande partie à Béjaïa (Bougie), l’une des capitales du Maghreb d’alors, où vivait son oncle Guillermo Bonacci. Celui-ci était le représentant, auprès des douanes maghrébines, des marchands toscans en Algérie, en Tunisie et au Maroc. Le jeune Leonardo, formé dans les écoles algériennes, s’est vite passionné pour les mathématiques arabes. Fibonacci rapporta à Pise en 1198 les chiffres arabes et la notation algébrique. Grâce à ses écrits et à sa persévérance, Fibonacci réussit là où le pape Sylvestre II échoua. 

L’introduction du papier, des chiffres arabes et de tout le savoir arabe en Europe va grandement faciliter la Renaissance européenne.

Hannibal Genséric